 Caractéristiques des Variables Aléatoires
Caractéristiques des Variables Aléatoires
Les caractéristiques des variables aléatoires sont importantes car elles fournissent un moyen formel de décrire et d'analyser le comportement des événements et résultats incertains dans un cadre probabiliste. Elles nous permettent de quantifier et de mesurer l'incertitude, la variabilité et la tendance centrale des variables aléatoires, ce qui est essentiel pour prendre des décisions éclairées et tirer des conclusions significatives à partir des données.
La distribution de probabilité d'une variable aléatoire
La distribution de probabilité d'une variable aléatoire spécifie les probabilités associées à chaque valeur possible dans son domaine. Elle peut être représentée à l'aide de la fonction de masse de probabilité (PMF) pour les variables aléatoires discrètes, ou de la fonction de densité de probabilité (PDF) pour les variables aléatoires continues. Nous avons considéré la PMF et la PDF dans le chapitre précédent.
Regardons la PDF de certaines distributions continues :
123456789101112131415161718192021222324252627import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm, expon, chi2 # Create subplots with 1 row and 3 columns fig, axes = plt.subplots(1, 3) # Set figure size fig.set_size_inches(10, 5) # Generate evenly spaced values for x-axis x = np.linspace(0, 10, 500) # Plot PDF of standard normal distribution on the first subplot axes[0].plot(x, norm.pdf(x, loc=5, scale=2)) axes[0].set_title('Standard Normal Distribution') # Plot PDF of exponential distribution on the second subplot axes[1].plot(x, expon.pdf(x)) axes[1].set_title('Exponential Distribution') # Plot PDF of chi-square distribution on the third subplot axes[2].plot(x, chi2.pdf(x, df=3)) axes[2].set_title('Chi-square Distribution') # Show the plot plt.show()
Valeur attendue
La valeur attendue, également connue sous le nom de moyenne ou moyenne arithmétique, d'une variable aléatoire est une mesure de la tendance centrale de la variable aléatoire. Elle représente la moyenne pondérée de toutes les valeurs possibles de la variable aléatoire, pondérées par leurs probabilités respectives.
Supposons que X soit une variable aléatoire discrète et que sa PMF ressemble à :
| Valeurs | x_1 | x_2 | x_3 | .... | x_N |
|---|---|---|---|---|---|
| Probabilité | p_1 | p_2 | p_3 | .... | p_N |
Nous pouvons calculer l'espérance comme suit :
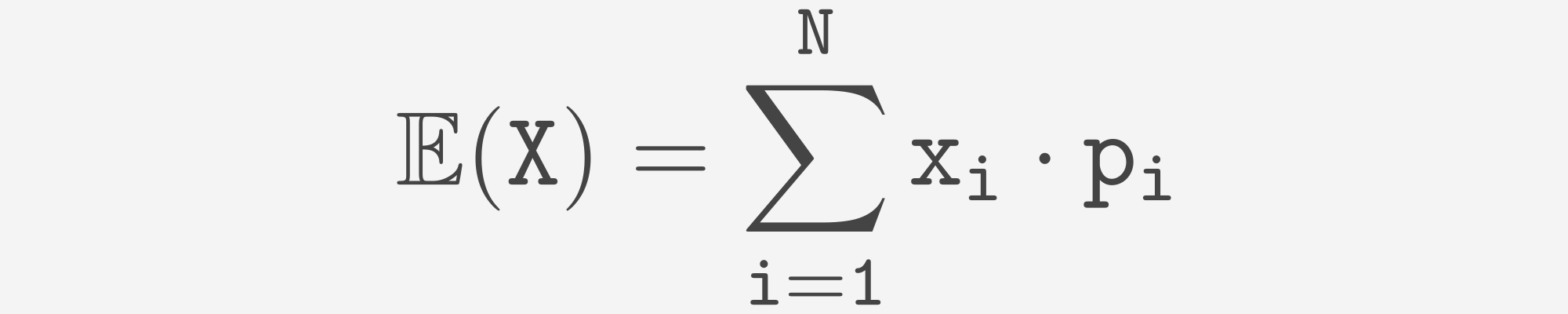
Calculons maintenant l'espérance pour une variable aléatoire continue X. En supposant que f(x) soit une PDF de cette variable, nous pouvons calculer l'espérance comme suit :
Regardons le tracé PDF de la distribution normale avec différentes moyennes :
1234567891011121314151617181920212223import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm # Create a figure object fig = plt.figure() # Set the size of the figure fig.set_size_inches(10, 5) # Generate evenly spaced values for the x-axis x = np.linspace(-10, 10, 500) # Plot three normal distributions with different means plt.plot(x, norm.pdf(x, loc=0, scale=2), label='Normal distribution with 0 mean') plt.plot(x, norm.pdf(x, loc=5, scale=2), label='Normal distribution with 5 mean') plt.plot(x, norm.pdf(x, loc=-5, scale=2), label='Normal distribution with -5 mean') # Add a legend to the plot plt.legend() # Show the plot plt.show()
Variance
La variance d'une variable aléatoire est une mesure de la dispersion ou de l'étalement des valeurs de la variable aléatoire autour de sa valeur espérée. Elle quantifie la variabilité ou l'incertitude associée à la variable aléatoire. Pour calculer la variance, nous pouvons utiliser la formule suivante :
Regardons le graphique PDF de la distribution normale avec différentes variances et une moyenne fixe :
12345678910111213141516171819202122232425import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm # Create a figure with 1 row and 3 columns of subplots, sharing the y-axis fig, axes = plt.subplots(1, 3, sharey=True) # Set the overall size of the figure fig.set_size_inches(10, 5) # Generate 500 points evenly spaced between -10 and 10 x = np.linspace(-10, 10, 500) # Plot normal distributions with different variances (controlled by 'scale') on each subplot axes[0].plot(x, norm.pdf(x, loc=0, scale=1)) # Variance = 1 (scale = std. dev) axes[1].plot(x, norm.pdf(x, loc=0, scale=3)) # Variance = 9 (std. dev = 3) axes[2].plot(x, norm.pdf(x, loc=0, scale=5)) # Variance = 25 (std. dev = 5) # Set titles for each subplot to indicate the variance axes[0].set_title('Variance = 1') axes[1].set_title('Variance = 9') axes[2].set_title('Variance = 25') # Display the plot with all three distributions plt.show()
La racine carrée de la variance est appelée écart-type. Utiliser l'écart-type au lieu de la variance peut être avantageux pour deux raisons :
- Nous travaillerons avec des valeurs absolues plus petites (alors que la variance sera, par exemple, 225, l'écart-type ne sera que de 15, ce qui est beaucoup plus pratique en termes de calculs) ;
- L'écart-type est mesuré dans les mêmes unités que les données, ce qui peut être important dans certains cas (si, par exemple, nous travaillons avec des longueurs en mètres, alors la variance sera mesurée en mètres carrés, tandis que l'écart-type est toujours en mètres).
Note
Le mot-clé
scalede la classescipy.stats.normreprésente l'écart-type de la distribution normale.
Le mot-clélocde la classescipy.stats.normreprésente la moyenne de la distribution normale.
Médiane
La médiane mesure la tendance centrale en statistiques qui représente la valeur centrale dans un ensemble de données lorsqu'il est classé par ordre croissant ou décroissant.
Nous pouvons calculer la médiane de la variable aléatoire X comme suit :
- Déterminer la CDF de
X; - Trouver la valeur y telle que CDF(
y) =0.5; - Cette valeur y est la médiane de la variable aléatoire
X.
Il est important de comprendre que la valeur espérée et la médiane sont deux caractéristiques différentes : la valeur espérée est la moyenne pondérée de toutes les valeurs possibles de la variable aléatoire, tandis que les poids sont les probabilités que ces valeurs se produisent ; d'autre part, la médiane est la valeur qui sépare les données en deux moitiés.
Pour les variables aléatoires avec des distributions asymétriques, cette différence est la plus significative.
Regardons l'exemple ci-dessous :
12345678910111213141516171819202122232425262728293031323334353637import numpy as np import matplotlib.pyplot as plt import scipy.stats as stats # Create subplots fig, axes = plt.subplots(1, 2) fig.set_size_inches(10, 5) # Calculate the expected value and median for exponential distribution expected_value_exp = stats.expon.mean(scale=2) median_exp = stats.expon.median(scale=2) # Calculate the expected value and median for chi-square distribution expected_value_chi = stats.chi2.mean(df=3) median_chi = stats.chi2.median(df=3) # Generate x values for plotting PDFs x = np.linspace(0, 10, 500) # Plot the PDFs axes[0].plot(x, stats.expon.pdf(x, scale=2), label='Exponential PDF') axes[1].plot(x, stats.chi2.pdf(x, df=3), label='Chi-square PDF') # Plot vertical lines for expected value and median axes[0].axvline(expected_value_exp, color='red', linestyle='--', label='Expected Value') axes[0].axvline(median_exp, color='green', linestyle='--', label='Median') axes[1].axvline(expected_value_chi, color='red', linestyle='--', label='Expected Value') axes[1].axvline(median_chi, color='green', linestyle='--', label='Median') # Set titles and legends axes[0].set_title('Exponential PDF with Expected Value and Median') axes[1].set_title('Chi-square PDF with Expected Value and Median') axes[0].legend() axes[1].legend() # Show the plots plt.show()
Nous voyons que la valeur espérée est décalée dans la direction de la queue de la distribution. Nous devons admettre que la valeur espérée est plus affectée par les valeurs aberrantes et les anomalies, ce qui rend cette caractéristique moins fiable pour l'analyse de données réelles.
Merci pour vos commentaires !
Demandez à l'IA
Demandez à l'IA

Posez n'importe quelle question ou essayez l'une des questions suggérées pour commencer notre discussion
Génial!
Completion taux amélioré à 3.7 Caractéristiques des Variables Aléatoires
Caractéristiques des Variables Aléatoires
Glissez pour afficher le menu
Les caractéristiques des variables aléatoires sont importantes car elles fournissent un moyen formel de décrire et d'analyser le comportement des événements et résultats incertains dans un cadre probabiliste. Elles nous permettent de quantifier et de mesurer l'incertitude, la variabilité et la tendance centrale des variables aléatoires, ce qui est essentiel pour prendre des décisions éclairées et tirer des conclusions significatives à partir des données.
La distribution de probabilité d'une variable aléatoire
La distribution de probabilité d'une variable aléatoire spécifie les probabilités associées à chaque valeur possible dans son domaine. Elle peut être représentée à l'aide de la fonction de masse de probabilité (PMF) pour les variables aléatoires discrètes, ou de la fonction de densité de probabilité (PDF) pour les variables aléatoires continues. Nous avons considéré la PMF et la PDF dans le chapitre précédent.
Regardons la PDF de certaines distributions continues :
123456789101112131415161718192021222324252627import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm, expon, chi2 # Create subplots with 1 row and 3 columns fig, axes = plt.subplots(1, 3) # Set figure size fig.set_size_inches(10, 5) # Generate evenly spaced values for x-axis x = np.linspace(0, 10, 500) # Plot PDF of standard normal distribution on the first subplot axes[0].plot(x, norm.pdf(x, loc=5, scale=2)) axes[0].set_title('Standard Normal Distribution') # Plot PDF of exponential distribution on the second subplot axes[1].plot(x, expon.pdf(x)) axes[1].set_title('Exponential Distribution') # Plot PDF of chi-square distribution on the third subplot axes[2].plot(x, chi2.pdf(x, df=3)) axes[2].set_title('Chi-square Distribution') # Show the plot plt.show()
Valeur attendue
La valeur attendue, également connue sous le nom de moyenne ou moyenne arithmétique, d'une variable aléatoire est une mesure de la tendance centrale de la variable aléatoire. Elle représente la moyenne pondérée de toutes les valeurs possibles de la variable aléatoire, pondérées par leurs probabilités respectives.
Supposons que X soit une variable aléatoire discrète et que sa PMF ressemble à :
| Valeurs | x_1 | x_2 | x_3 | .... | x_N |
|---|---|---|---|---|---|
| Probabilité | p_1 | p_2 | p_3 | .... | p_N |
Nous pouvons calculer l'espérance comme suit :
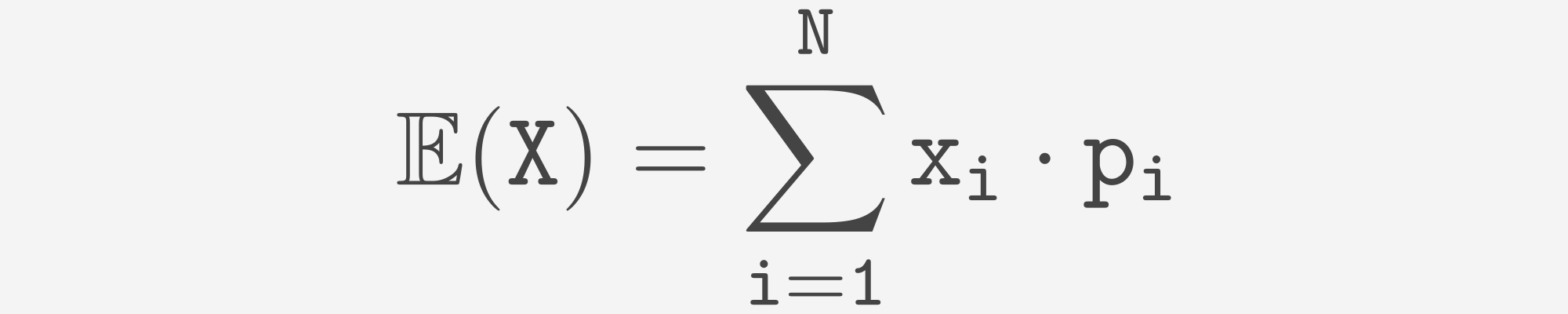
Calculons maintenant l'espérance pour une variable aléatoire continue X. En supposant que f(x) soit une PDF de cette variable, nous pouvons calculer l'espérance comme suit :
Regardons le tracé PDF de la distribution normale avec différentes moyennes :
1234567891011121314151617181920212223import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm # Create a figure object fig = plt.figure() # Set the size of the figure fig.set_size_inches(10, 5) # Generate evenly spaced values for the x-axis x = np.linspace(-10, 10, 500) # Plot three normal distributions with different means plt.plot(x, norm.pdf(x, loc=0, scale=2), label='Normal distribution with 0 mean') plt.plot(x, norm.pdf(x, loc=5, scale=2), label='Normal distribution with 5 mean') plt.plot(x, norm.pdf(x, loc=-5, scale=2), label='Normal distribution with -5 mean') # Add a legend to the plot plt.legend() # Show the plot plt.show()
Variance
La variance d'une variable aléatoire est une mesure de la dispersion ou de l'étalement des valeurs de la variable aléatoire autour de sa valeur espérée. Elle quantifie la variabilité ou l'incertitude associée à la variable aléatoire. Pour calculer la variance, nous pouvons utiliser la formule suivante :
Regardons le graphique PDF de la distribution normale avec différentes variances et une moyenne fixe :
12345678910111213141516171819202122232425import numpy as np import matplotlib.pyplot as plt from scipy.stats import norm # Create a figure with 1 row and 3 columns of subplots, sharing the y-axis fig, axes = plt.subplots(1, 3, sharey=True) # Set the overall size of the figure fig.set_size_inches(10, 5) # Generate 500 points evenly spaced between -10 and 10 x = np.linspace(-10, 10, 500) # Plot normal distributions with different variances (controlled by 'scale') on each subplot axes[0].plot(x, norm.pdf(x, loc=0, scale=1)) # Variance = 1 (scale = std. dev) axes[1].plot(x, norm.pdf(x, loc=0, scale=3)) # Variance = 9 (std. dev = 3) axes[2].plot(x, norm.pdf(x, loc=0, scale=5)) # Variance = 25 (std. dev = 5) # Set titles for each subplot to indicate the variance axes[0].set_title('Variance = 1') axes[1].set_title('Variance = 9') axes[2].set_title('Variance = 25') # Display the plot with all three distributions plt.show()
La racine carrée de la variance est appelée écart-type. Utiliser l'écart-type au lieu de la variance peut être avantageux pour deux raisons :
- Nous travaillerons avec des valeurs absolues plus petites (alors que la variance sera, par exemple, 225, l'écart-type ne sera que de 15, ce qui est beaucoup plus pratique en termes de calculs) ;
- L'écart-type est mesuré dans les mêmes unités que les données, ce qui peut être important dans certains cas (si, par exemple, nous travaillons avec des longueurs en mètres, alors la variance sera mesurée en mètres carrés, tandis que l'écart-type est toujours en mètres).
Note
Le mot-clé
scalede la classescipy.stats.normreprésente l'écart-type de la distribution normale.
Le mot-clélocde la classescipy.stats.normreprésente la moyenne de la distribution normale.
Médiane
La médiane mesure la tendance centrale en statistiques qui représente la valeur centrale dans un ensemble de données lorsqu'il est classé par ordre croissant ou décroissant.
Nous pouvons calculer la médiane de la variable aléatoire X comme suit :
- Déterminer la CDF de
X; - Trouver la valeur y telle que CDF(
y) =0.5; - Cette valeur y est la médiane de la variable aléatoire
X.
Il est important de comprendre que la valeur espérée et la médiane sont deux caractéristiques différentes : la valeur espérée est la moyenne pondérée de toutes les valeurs possibles de la variable aléatoire, tandis que les poids sont les probabilités que ces valeurs se produisent ; d'autre part, la médiane est la valeur qui sépare les données en deux moitiés.
Pour les variables aléatoires avec des distributions asymétriques, cette différence est la plus significative.
Regardons l'exemple ci-dessous :
12345678910111213141516171819202122232425262728293031323334353637import numpy as np import matplotlib.pyplot as plt import scipy.stats as stats # Create subplots fig, axes = plt.subplots(1, 2) fig.set_size_inches(10, 5) # Calculate the expected value and median for exponential distribution expected_value_exp = stats.expon.mean(scale=2) median_exp = stats.expon.median(scale=2) # Calculate the expected value and median for chi-square distribution expected_value_chi = stats.chi2.mean(df=3) median_chi = stats.chi2.median(df=3) # Generate x values for plotting PDFs x = np.linspace(0, 10, 500) # Plot the PDFs axes[0].plot(x, stats.expon.pdf(x, scale=2), label='Exponential PDF') axes[1].plot(x, stats.chi2.pdf(x, df=3), label='Chi-square PDF') # Plot vertical lines for expected value and median axes[0].axvline(expected_value_exp, color='red', linestyle='--', label='Expected Value') axes[0].axvline(median_exp, color='green', linestyle='--', label='Median') axes[1].axvline(expected_value_chi, color='red', linestyle='--', label='Expected Value') axes[1].axvline(median_chi, color='green', linestyle='--', label='Median') # Set titles and legends axes[0].set_title('Exponential PDF with Expected Value and Median') axes[1].set_title('Chi-square PDF with Expected Value and Median') axes[0].legend() axes[1].legend() # Show the plots plt.show()
Nous voyons que la valeur espérée est décalée dans la direction de la queue de la distribution. Nous devons admettre que la valeur espérée est plus affectée par les valeurs aberrantes et les anomalies, ce qui rend cette caractéristique moins fiable pour l'analyse de données réelles.
Merci pour vos commentaires !