 Лінійна алгебра
Лінійна алгебра
Операції лінійної алгебри
TensorFlow надає набір функцій, призначених для операцій лінійної алгебри, що спрощує виконання матричних операцій.
Множення матриць
Коротке нагадування про те, як працює множення матриць.
Існує два еквівалентних підходи до множення матриць:
- Функція
tf.matmul(); - Використання оператора
@.
1234567891011121314import tensorflow as tf # Create two matrices matrix1 = tf.constant([[1, 2], [3, 4], [2, 1]]) matrix2 = tf.constant([[2, 0, 2, 5], [2, 2, 1, 3]]) # Multiply the matrices product1 = tf.matmul(matrix1, matrix2) product2 = matrix1 @ matrix2 # Display tensors print(product1) print('-' * 50) print(product2)
Множення матриць розмірів 3x2 та 2x4 дає матрицю розміру 3x4.
Інверсія матриці
Інверсію матриці можна отримати за допомогою функції tf.linalg.inv(). Додатково перевіримо фундаментальну властивість оберненої матриці.
123456789101112131415import tensorflow as tf # Create 2x2 matrix matrix = tf.constant([[1., 2.], [3., 4.]]) # Compute the inverse of a matrix inverse_mat = tf.linalg.inv(matrix) # Check the result identity = matrix @ inverse_mat # Display tensors print(inverse_mat) print('-' * 50) print(identity)
Множення матриці на її обернену має давати одиничну матрицю, у якої на головній діагоналі стоять одиниці, а всі інші елементи дорівнюють нулю. Крім того, модуль tf.linalg містить широкий спектр функцій для лінійної алгебри. Для отримання додаткової інформації або виконання більш складних операцій рекомендується звернутися до офіційної документації.
Транспонування
Транспоновану матрицю можна отримати за допомогою функції tf.transpose().
123456789101112import tensorflow as tf # Create a matrix 3x2 matrix = tf.constant([[1, 2], [3, 4], [2, 1]]) # Get the transpose of a matrix transposed = tf.transpose(matrix) # Display tensors print(matrix) print('-' * 40) print(transposed)
Скалярний добуток
Скалярний добуток можна отримати за допомогою функції tf.tensordot(). Встановлюючи аргумент axes, можна обрати, по яких осях обчислювати скалярний добуток. Наприклад, для двох векторів, встановивши axes=1, ви отримаєте класичний скалярний добуток між векторами. Але якщо встановити axes=0, ви отримаєте розширену матрицю по осі 0:
1234567891011121314import tensorflow as tf # Create two vectors matrix1 = tf.constant([1, 2, 3, 4]) matrix2 = tf.constant([2, 0, 2, 5]) # Compute the dot product of two tensors dot_product_axes1 = tf.tensordot(matrix1, matrix2, axes=1) dot_product_axes0 = tf.tensordot(matrix1, matrix2, axes=0) # Display tensors print(dot_product_axes1) print('-' * 40) print(dot_product_axes0)
Якщо взяти дві матриці з відповідними розмірами (NxM @ MxK, де NxM — розміри першої матриці, а MxK — другої), і обчислити скалярний добуток по axes=1, це фактично виконує множення матриць.
Swipe to start coding
Теоретичні відомості
Систему лінійних рівнянь можна представити у матричній формі за допомогою рівняння:
AX = B
Де:
A— матриця коефіцієнтів;X— стовпчикова матриця змінних;B— стовпчикова матриця, що містить значення з правої частини рівнянь.
Розв'язок цієї системи можна знайти за формулою:
X = A^-1 B
де A^-1 — обернена матриця до A.
Мета
Для заданої системи лінійних рівнянь використати TensorFlow для її розв'язання. Дано таку систему лінійних рівнянь:
2x + 3y - z = 1.4x + y + 2z = 2.-x + 2y + 3z = 3.
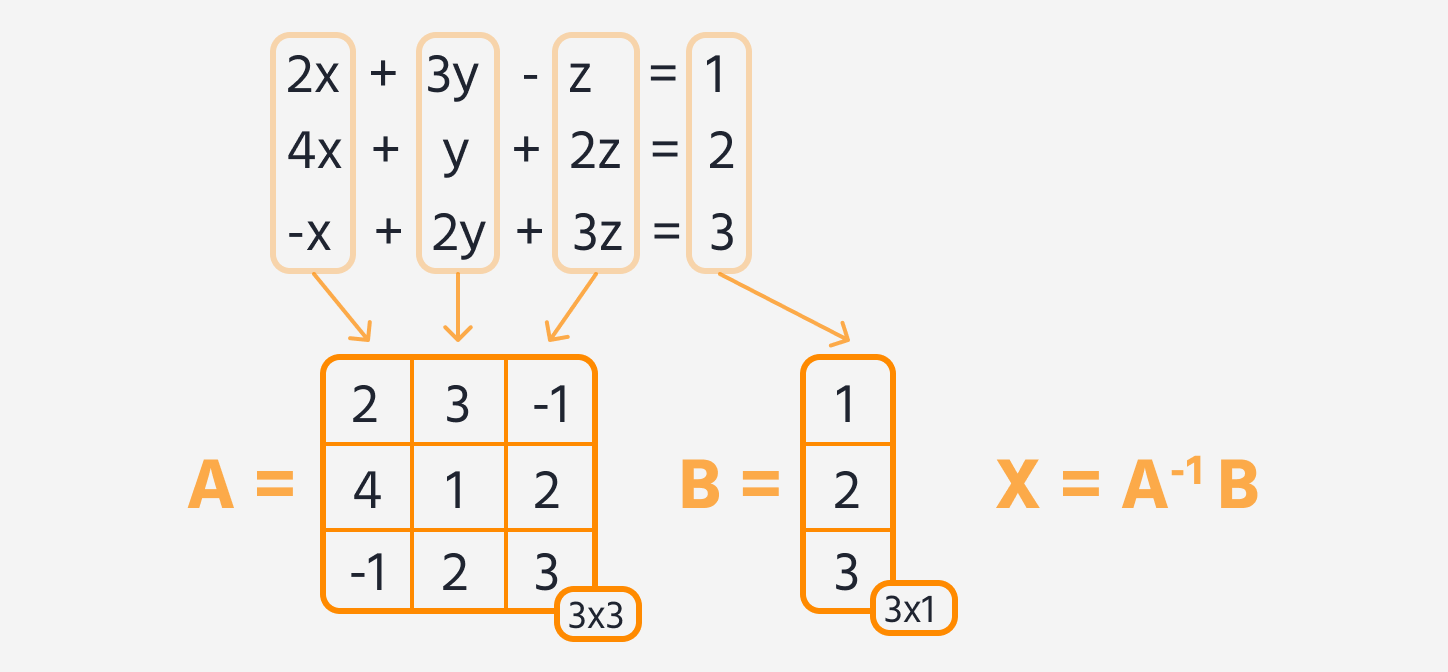
- Представити систему рівнянь у матричній формі (розділити на матриці
AтаB). - За допомогою TensorFlow знайти обернену матрицю
A. - Перемножити обернену матрицю
Aна матрицюB, щоб знайти матрицю розв'язківX, яка містить значенняx,yтаz.
Примітка
Зрізи (slicing) у TensorFlow працюють подібно до NumPy. Тому
X[:, 0]поверне всі елементи зі стовпця з індексом0. До зрізів ми повернемося пізніше у курсі.
Рішення
Дякуємо за ваш відгук!
single
Запитати АІ
Запитати АІ

Запитайте про що завгодно або спробуйте одне із запропонованих запитань, щоб почати наш чат
Can you explain the difference between tf.matmul() and the @ operator?
How do I know when to use tf.tensordot() instead of tf.matmul()?
Can you provide more examples of matrix operations in TensorFlow?

Чудово!
Completion показник покращився до 6.25 Лінійна алгебра
Лінійна алгебра
Свайпніть щоб показати меню
Операції лінійної алгебри
TensorFlow надає набір функцій, призначених для операцій лінійної алгебри, що спрощує виконання матричних операцій.
Множення матриць
Коротке нагадування про те, як працює множення матриць.
Існує два еквівалентних підходи до множення матриць:
- Функція
tf.matmul(); - Використання оператора
@.
1234567891011121314import tensorflow as tf # Create two matrices matrix1 = tf.constant([[1, 2], [3, 4], [2, 1]]) matrix2 = tf.constant([[2, 0, 2, 5], [2, 2, 1, 3]]) # Multiply the matrices product1 = tf.matmul(matrix1, matrix2) product2 = matrix1 @ matrix2 # Display tensors print(product1) print('-' * 50) print(product2)
Множення матриць розмірів 3x2 та 2x4 дає матрицю розміру 3x4.
Інверсія матриці
Інверсію матриці можна отримати за допомогою функції tf.linalg.inv(). Додатково перевіримо фундаментальну властивість оберненої матриці.
123456789101112131415import tensorflow as tf # Create 2x2 matrix matrix = tf.constant([[1., 2.], [3., 4.]]) # Compute the inverse of a matrix inverse_mat = tf.linalg.inv(matrix) # Check the result identity = matrix @ inverse_mat # Display tensors print(inverse_mat) print('-' * 50) print(identity)
Множення матриці на її обернену має давати одиничну матрицю, у якої на головній діагоналі стоять одиниці, а всі інші елементи дорівнюють нулю. Крім того, модуль tf.linalg містить широкий спектр функцій для лінійної алгебри. Для отримання додаткової інформації або виконання більш складних операцій рекомендується звернутися до офіційної документації.
Транспонування
Транспоновану матрицю можна отримати за допомогою функції tf.transpose().
123456789101112import tensorflow as tf # Create a matrix 3x2 matrix = tf.constant([[1, 2], [3, 4], [2, 1]]) # Get the transpose of a matrix transposed = tf.transpose(matrix) # Display tensors print(matrix) print('-' * 40) print(transposed)
Скалярний добуток
Скалярний добуток можна отримати за допомогою функції tf.tensordot(). Встановлюючи аргумент axes, можна обрати, по яких осях обчислювати скалярний добуток. Наприклад, для двох векторів, встановивши axes=1, ви отримаєте класичний скалярний добуток між векторами. Але якщо встановити axes=0, ви отримаєте розширену матрицю по осі 0:
1234567891011121314import tensorflow as tf # Create two vectors matrix1 = tf.constant([1, 2, 3, 4]) matrix2 = tf.constant([2, 0, 2, 5]) # Compute the dot product of two tensors dot_product_axes1 = tf.tensordot(matrix1, matrix2, axes=1) dot_product_axes0 = tf.tensordot(matrix1, matrix2, axes=0) # Display tensors print(dot_product_axes1) print('-' * 40) print(dot_product_axes0)
Якщо взяти дві матриці з відповідними розмірами (NxM @ MxK, де NxM — розміри першої матриці, а MxK — другої), і обчислити скалярний добуток по axes=1, це фактично виконує множення матриць.
Swipe to start coding
Теоретичні відомості
Систему лінійних рівнянь можна представити у матричній формі за допомогою рівняння:
AX = B
Де:
A— матриця коефіцієнтів;X— стовпчикова матриця змінних;B— стовпчикова матриця, що містить значення з правої частини рівнянь.
Розв'язок цієї системи можна знайти за формулою:
X = A^-1 B
де A^-1 — обернена матриця до A.
Мета
Для заданої системи лінійних рівнянь використати TensorFlow для її розв'язання. Дано таку систему лінійних рівнянь:
2x + 3y - z = 1.4x + y + 2z = 2.-x + 2y + 3z = 3.

- Представити систему рівнянь у матричній формі (розділити на матриці
AтаB). - За допомогою TensorFlow знайти обернену матрицю
A. - Перемножити обернену матрицю
Aна матрицюB, щоб знайти матрицю розв'язківX, яка містить значенняx,yтаz.
Примітка
Зрізи (slicing) у TensorFlow працюють подібно до NumPy. Тому
X[:, 0]поверне всі елементи зі стовпця з індексом0. До зрізів ми повернемося пізніше у курсі.
Рішення
Дякуємо за ваш відгук!
single