 Comparing the Trends Across Clusters
Comparing the Trends Across Clusters
Both cases look correct, or at least there is nothing wrong. Let's compare the dynamics across months for both cases.
You might remember from the previous sections how the algorithms predicted the dynamics. The spectral clustering with 4 clusters will predict the following dynamics.
12345678910111213141516171819202122232425262728# Import the librarires import pandas as pd import seaborn as sns import matplotlib.pyplot as plt from sklearn.cluster import SpectralClustering # Read the data data = pd.read_csv('https://codefinity-content-media.s3.eu-west-1.amazonaws.com/138ab9ad-aa37-4310-873f-0f62abafb038/Cities+weather.csv', index_col = 0) # Create the model model = SpectralClustering(n_clusters = 4, affinity = 'nearest_neighbors') # Fit the data and predict the labels data['prediction'] = model.fit_predict(data.iloc[:,2:14]) # Extract the list of the columns col = list(data.columns[2:14]) col.append('prediction') # Calculate the monthly mean averages for each cluster d = data[col].groupby('prediction').mean().stack().reset_index() # Assign new column names d.columns = ['Group', 'Month', "Temp"] # Visualize the results sns.lineplot(x = 'Month', y = "Temp", hue = 'Group', data = d) plt.show()
Quite an interesting result! The spectral clustering algorithm catches the 'downwards` up to summer dynamics even in the case of 4 clusters. Let's find out what will be the fifth line produced by this algorithm.
Swipe to start coding
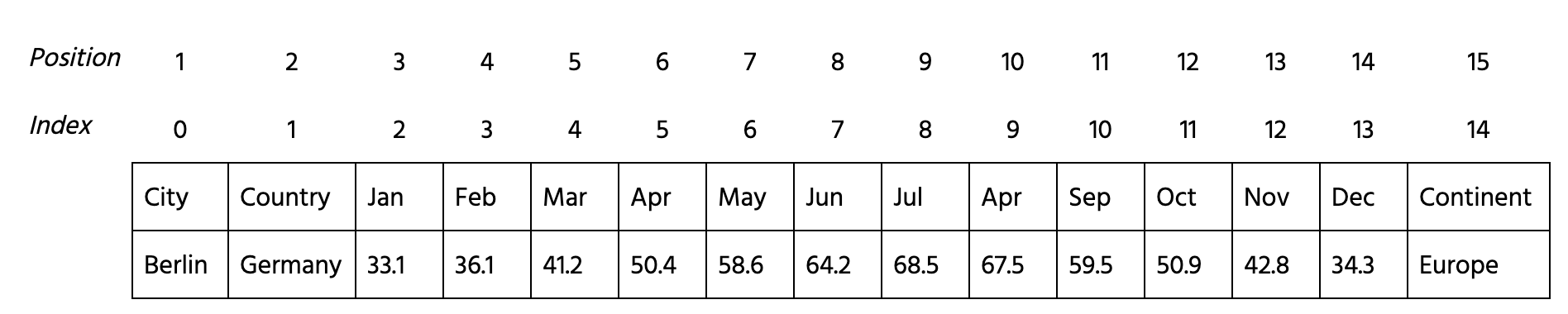
- Import
SpectralClusteringfunction fromsklearn.cluster. - Create
SpectralClusteringmodel namedmodelwith 5 clusters and'nearest_neighbors'affinity. - Fit the 3-14 columns of
datatomodeland predict labels. Save them within'prediction'column ofdata. - Calculate the mean for each month within the
monthly_datavariable:
- Group the observation of
colcolumns by the'prediction'column. - Calculate the mean within each group.
- Stack the table.
- Reset the indices.
- Reassign the column names of newly created DataFrame
monthly_datato['Group', 'Month', 'Temp']. - Build
seabornline plot'Month'vs'Temp'for each'Group'value. Display the plot.
Solução
Obrigado pelo seu feedback!
single
Pergunte à IA
Pergunte à IA

Pergunte o que quiser ou experimente uma das perguntas sugeridas para iniciar nosso bate-papo

Incrível!
Completion taxa melhorada para 3.57 Comparing the Trends Across Clusters
Comparing the Trends Across Clusters
Deslize para mostrar o menu
Both cases look correct, or at least there is nothing wrong. Let's compare the dynamics across months for both cases.
You might remember from the previous sections how the algorithms predicted the dynamics. The spectral clustering with 4 clusters will predict the following dynamics.
12345678910111213141516171819202122232425262728# Import the librarires import pandas as pd import seaborn as sns import matplotlib.pyplot as plt from sklearn.cluster import SpectralClustering # Read the data data = pd.read_csv('https://codefinity-content-media.s3.eu-west-1.amazonaws.com/138ab9ad-aa37-4310-873f-0f62abafb038/Cities+weather.csv', index_col = 0) # Create the model model = SpectralClustering(n_clusters = 4, affinity = 'nearest_neighbors') # Fit the data and predict the labels data['prediction'] = model.fit_predict(data.iloc[:,2:14]) # Extract the list of the columns col = list(data.columns[2:14]) col.append('prediction') # Calculate the monthly mean averages for each cluster d = data[col].groupby('prediction').mean().stack().reset_index() # Assign new column names d.columns = ['Group', 'Month', "Temp"] # Visualize the results sns.lineplot(x = 'Month', y = "Temp", hue = 'Group', data = d) plt.show()
Quite an interesting result! The spectral clustering algorithm catches the 'downwards` up to summer dynamics even in the case of 4 clusters. Let's find out what will be the fifth line produced by this algorithm.
Swipe to start coding

- Import
SpectralClusteringfunction fromsklearn.cluster. - Create
SpectralClusteringmodel namedmodelwith 5 clusters and'nearest_neighbors'affinity. - Fit the 3-14 columns of
datatomodeland predict labels. Save them within'prediction'column ofdata. - Calculate the mean for each month within the
monthly_datavariable:
- Group the observation of
colcolumns by the'prediction'column. - Calculate the mean within each group.
- Stack the table.
- Reset the indices.
- Reassign the column names of newly created DataFrame
monthly_datato['Group', 'Month', 'Temp']. - Build
seabornline plot'Month'vs'Temp'for each'Group'value. Display the plot.
Solução
Obrigado pelo seu feedback!
single