 Algèbre Linéaire
Algèbre Linéaire
Opérations d'algèbre linéaire
TensorFlow propose un ensemble de fonctions dédiées aux opérations d'algèbre linéaire, facilitant ainsi les opérations matricielles.
Multiplication de matrices
Rappel rapide sur le fonctionnement de la multiplication de matrices.
Il existe deux approches équivalentes pour la multiplication de matrices :
- La fonction
tf.matmul(); - L'utilisation de l'opérateur
@.
1234567891011121314import tensorflow as tf # Create two matrices matrix1 = tf.constant([[1, 2], [3, 4], [2, 1]]) matrix2 = tf.constant([[2, 0, 2, 5], [2, 2, 1, 3]]) # Multiply the matrices product1 = tf.matmul(matrix1, matrix2) product2 = matrix1 @ matrix2 # Display tensors print(product1) print('-' * 50) print(product2)
La multiplication de matrices de taille 3x2 et 2x4 donne une matrice de 3x4.
Inversion de matrice
L'inverse d'une matrice peut être obtenue à l'aide de la fonction tf.linalg.inv(). Vérification d'une propriété fondamentale de la matrice inverse.
123456789101112131415import tensorflow as tf # Create 2x2 matrix matrix = tf.constant([[1., 2.], [3., 4.]]) # Compute the inverse of a matrix inverse_mat = tf.linalg.inv(matrix) # Check the result identity = matrix @ inverse_mat # Display tensors print(inverse_mat) print('-' * 50) print(identity)
La multiplication d'une matrice par son inverse doit donner une matrice identité, qui possède des uns sur sa diagonale principale et des zéros ailleurs. De plus, le module tf.linalg propose un large éventail de fonctions d’algèbre linéaire. Pour plus de détails ou des opérations plus avancées, il est conseillé de consulter sa documentation officielle.
Transposée
Il est possible d’obtenir une matrice transposée à l’aide de la fonction tf.transpose().
123456789101112import tensorflow as tf # Create a matrix 3x2 matrix = tf.constant([[1, 2], [3, 4], [2, 1]]) # Get the transpose of a matrix transposed = tf.transpose(matrix) # Display tensors print(matrix) print('-' * 40) print(transposed)
Produit scalaire
Le produit scalaire peut être obtenu à l'aide de la fonction tf.tensordot(). En configurant l'argument axes, il est possible de choisir selon quels axes calculer le produit scalaire. Par exemple, pour deux vecteurs, en définissant axes=1, on obtient le produit scalaire classique entre vecteurs. Mais en définissant axes=0, on obtient une matrice diffusée le long de l'axe 0 :
1234567891011121314import tensorflow as tf # Create two vectors matrix1 = tf.constant([1, 2, 3, 4]) matrix2 = tf.constant([2, 0, 2, 5]) # Compute the dot product of two tensors dot_product_axes1 = tf.tensordot(matrix1, matrix2, axes=1) dot_product_axes0 = tf.tensordot(matrix1, matrix2, axes=0) # Display tensors print(dot_product_axes1) print('-' * 40) print(dot_product_axes0)
Si vous prenez deux matrices avec des dimensions appropriées (NxM @ MxK, où NxM représente les dimensions de la première matrice et MxK celles de la seconde), et que vous calculez le produit scalaire selon axes=1, cela réalise essentiellement une multiplication matricielle.
Swipe to start coding
Contexte
Un système d'équations linéaires peut être représenté sous forme matricielle à l'aide de l'équation :
AX = B
Où :
Aest une matrice de coefficients ;Xest une matrice colonne des variables ;Best une matrice colonne représentant les valeurs du côté droit des équations.
La solution de ce système peut être trouvée à l'aide de la formule :
X = A^-1 B
Où A^-1 est l'inverse de la matrice A.
Objectif
Étant donné un système d'équations linéaires, utiliser TensorFlow pour le résoudre. Le système d'équations linéaires suivant vous est donné :
2x + 3y - z = 1.4x + y + 2z = 2.-x + 2y + 3z = 3.
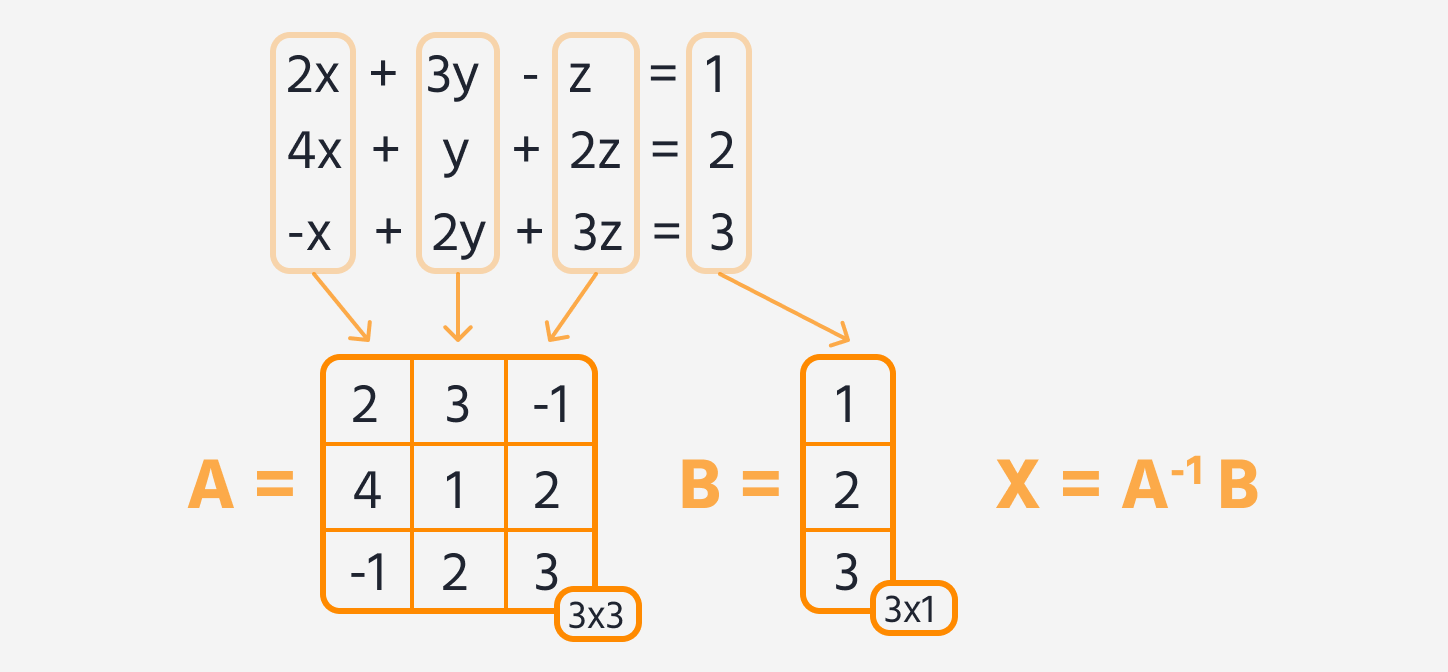
- Représenter le système d'équations sous forme matricielle (séparer en matrices
AetB). - À l'aide de TensorFlow, trouver l'inverse de la matrice
A. - Multiplier l'inverse de la matrice
Apar la matriceBpour obtenir la matrice solutionX, qui contient les valeurs dex,yetz.
Remarque
Le découpage (slicing) dans TensorFlow fonctionne de manière similaire à NumPy. Ainsi,
X[:, 0]permet de récupérer tous les éléments de la colonne à l'indice0. Nous aborderons le découpage plus tard dans le cours.
Solution
Merci pour vos commentaires !
single
Demandez à l'IA
Demandez à l'IA

Posez n'importe quelle question ou essayez l'une des questions suggérées pour commencer notre discussion

Génial!
Completion taux amélioré à 6.25 Algèbre Linéaire
Algèbre Linéaire
Glissez pour afficher le menu
Opérations d'algèbre linéaire
TensorFlow propose un ensemble de fonctions dédiées aux opérations d'algèbre linéaire, facilitant ainsi les opérations matricielles.
Multiplication de matrices
Rappel rapide sur le fonctionnement de la multiplication de matrices.
Il existe deux approches équivalentes pour la multiplication de matrices :
- La fonction
tf.matmul(); - L'utilisation de l'opérateur
@.
1234567891011121314import tensorflow as tf # Create two matrices matrix1 = tf.constant([[1, 2], [3, 4], [2, 1]]) matrix2 = tf.constant([[2, 0, 2, 5], [2, 2, 1, 3]]) # Multiply the matrices product1 = tf.matmul(matrix1, matrix2) product2 = matrix1 @ matrix2 # Display tensors print(product1) print('-' * 50) print(product2)
La multiplication de matrices de taille 3x2 et 2x4 donne une matrice de 3x4.
Inversion de matrice
L'inverse d'une matrice peut être obtenue à l'aide de la fonction tf.linalg.inv(). Vérification d'une propriété fondamentale de la matrice inverse.
123456789101112131415import tensorflow as tf # Create 2x2 matrix matrix = tf.constant([[1., 2.], [3., 4.]]) # Compute the inverse of a matrix inverse_mat = tf.linalg.inv(matrix) # Check the result identity = matrix @ inverse_mat # Display tensors print(inverse_mat) print('-' * 50) print(identity)
La multiplication d'une matrice par son inverse doit donner une matrice identité, qui possède des uns sur sa diagonale principale et des zéros ailleurs. De plus, le module tf.linalg propose un large éventail de fonctions d’algèbre linéaire. Pour plus de détails ou des opérations plus avancées, il est conseillé de consulter sa documentation officielle.
Transposée
Il est possible d’obtenir une matrice transposée à l’aide de la fonction tf.transpose().
123456789101112import tensorflow as tf # Create a matrix 3x2 matrix = tf.constant([[1, 2], [3, 4], [2, 1]]) # Get the transpose of a matrix transposed = tf.transpose(matrix) # Display tensors print(matrix) print('-' * 40) print(transposed)
Produit scalaire
Le produit scalaire peut être obtenu à l'aide de la fonction tf.tensordot(). En configurant l'argument axes, il est possible de choisir selon quels axes calculer le produit scalaire. Par exemple, pour deux vecteurs, en définissant axes=1, on obtient le produit scalaire classique entre vecteurs. Mais en définissant axes=0, on obtient une matrice diffusée le long de l'axe 0 :
1234567891011121314import tensorflow as tf # Create two vectors matrix1 = tf.constant([1, 2, 3, 4]) matrix2 = tf.constant([2, 0, 2, 5]) # Compute the dot product of two tensors dot_product_axes1 = tf.tensordot(matrix1, matrix2, axes=1) dot_product_axes0 = tf.tensordot(matrix1, matrix2, axes=0) # Display tensors print(dot_product_axes1) print('-' * 40) print(dot_product_axes0)
Si vous prenez deux matrices avec des dimensions appropriées (NxM @ MxK, où NxM représente les dimensions de la première matrice et MxK celles de la seconde), et que vous calculez le produit scalaire selon axes=1, cela réalise essentiellement une multiplication matricielle.
Swipe to start coding
Contexte
Un système d'équations linéaires peut être représenté sous forme matricielle à l'aide de l'équation :
AX = B
Où :
Aest une matrice de coefficients ;Xest une matrice colonne des variables ;Best une matrice colonne représentant les valeurs du côté droit des équations.
La solution de ce système peut être trouvée à l'aide de la formule :
X = A^-1 B
Où A^-1 est l'inverse de la matrice A.
Objectif
Étant donné un système d'équations linéaires, utiliser TensorFlow pour le résoudre. Le système d'équations linéaires suivant vous est donné :
2x + 3y - z = 1.4x + y + 2z = 2.-x + 2y + 3z = 3.

- Représenter le système d'équations sous forme matricielle (séparer en matrices
AetB). - À l'aide de TensorFlow, trouver l'inverse de la matrice
A. - Multiplier l'inverse de la matrice
Apar la matriceBpour obtenir la matrice solutionX, qui contient les valeurs dex,yetz.
Remarque
Le découpage (slicing) dans TensorFlow fonctionne de manière similaire à NumPy. Ainsi,
X[:, 0]permet de récupérer tous les éléments de la colonne à l'indice0. Nous aborderons le découpage plus tard dans le cours.
Solution
Merci pour vos commentaires !
single