Operaciones de Álgebra Lineal

TensorFlow ofrece un conjunto de funciones dedicadas a las operaciones de álgebra lineal, facilitando las operaciones con matrices.

Multiplicación de Matrices

A continuación, un recordatorio rápido de cómo funciona la multiplicación de matrices.

Existen dos enfoques equivalentes para la multiplicación de matrices:

La función tf.matmul();
Usar el operador @.


              1234567891011121314
            
import tensorflow as tf

# Create two matrices
matrix1 = tf.constant([[1, 2], [3, 4], [2, 1]])
matrix2 = tf.constant([[2, 0, 2, 5], [2, 2, 1, 3]])

# Multiply the matrices
product1 = tf.matmul(matrix1, matrix2)
product2 = matrix1 @ matrix2

# Display tensors
print(product1)
print('-' * 50)
print(product2)

Nota

Multiplicar matrices de tamaño 3x2 y 2x4 dará como resultado una matriz de 3x4.

Inversión de matrices

Se puede obtener la inversa de una matriz utilizando la función tf.linalg.inv(). Además, verifiquemos una propiedad fundamental de la matriz inversa.


              123456789101112131415
            
import tensorflow as tf

# Create 2x2 matrix
matrix = tf.constant([[1., 2.], [3., 4.]])

# Compute the inverse of a matrix
inverse_mat = tf.linalg.inv(matrix)

# Check the result
identity = matrix @ inverse_mat

# Display tensors
print(inverse_mat)
print('-' * 50)
print(identity)

Nota

Multiplicar una matriz por su inversa debe producir una matriz identidad, que tiene unos en su diagonal principal y ceros en el resto de posiciones. Además, el módulo tf.linalg ofrece una amplia gama de funciones de álgebra lineal. Para obtener más detalles o realizar operaciones avanzadas, consulte su documentación oficial.

Transposición

Se puede obtener una matriz transpuesta utilizando la función tf.transpose().


              123456789101112
            
import tensorflow as tf

# Create a matrix 3x2
matrix = tf.constant([[1, 2], [3, 4], [2, 1]])

# Get the transpose of a matrix
transposed = tf.transpose(matrix)

# Display tensors
print(matrix)
print('-' * 40)
print(transposed)

Producto punto

Se puede obtener un producto punto utilizando la función tf.tensordot(). Al configurar un argumento axes, es posible elegir a lo largo de qué ejes calcular un producto punto. Por ejemplo, para dos vectores, al establecer axes=1 se obtiene el producto punto clásico entre vectores. Pero al establecer axes=0, se obtiene una matriz transmitida a lo largo del eje 0:


              1234567891011121314
            
import tensorflow as tf

# Create two vectors
matrix1 = tf.constant([1, 2, 3, 4])
matrix2 = tf.constant([2, 0, 2, 5])

# Compute the dot product of two tensors
dot_product_axes1 = tf.tensordot(matrix1, matrix2, axes=1)
dot_product_axes0 = tf.tensordot(matrix1, matrix2, axes=0)

# Display tensors
print(dot_product_axes1)
print('-' * 40)
print(dot_product_axes0)

Nota

Si se toman dos matrices con dimensiones apropiadas (NxM @ MxK, donde NxM representa las dimensiones de la primera matriz y MxK las de la segunda), y se calcula el producto punto a lo largo de axes=1, esto realiza esencialmente una multiplicación de matrices.

Tarea

Swipe to start coding

Contexto

Un sistema de ecuaciones lineales puede representarse en forma matricial utilizando la ecuación:

AX = B

Donde:

A es una matriz de coeficientes;
X es una matriz columna de variables;
B es una matriz columna que representa los valores en el lado derecho de las ecuaciones.

La solución de este sistema se puede encontrar usando la fórmula:

X = A^-1 B

Donde A^-1 es la inversa de la matriz A.

Objetivo

Dado un sistema de ecuaciones lineales, utilizar TensorFlow para resolverlo. Se proporciona el siguiente sistema de ecuaciones lineales:

2x + 3y - z = 1.
4x + y + 2z = 2.
-x + 2y + 3z = 3.

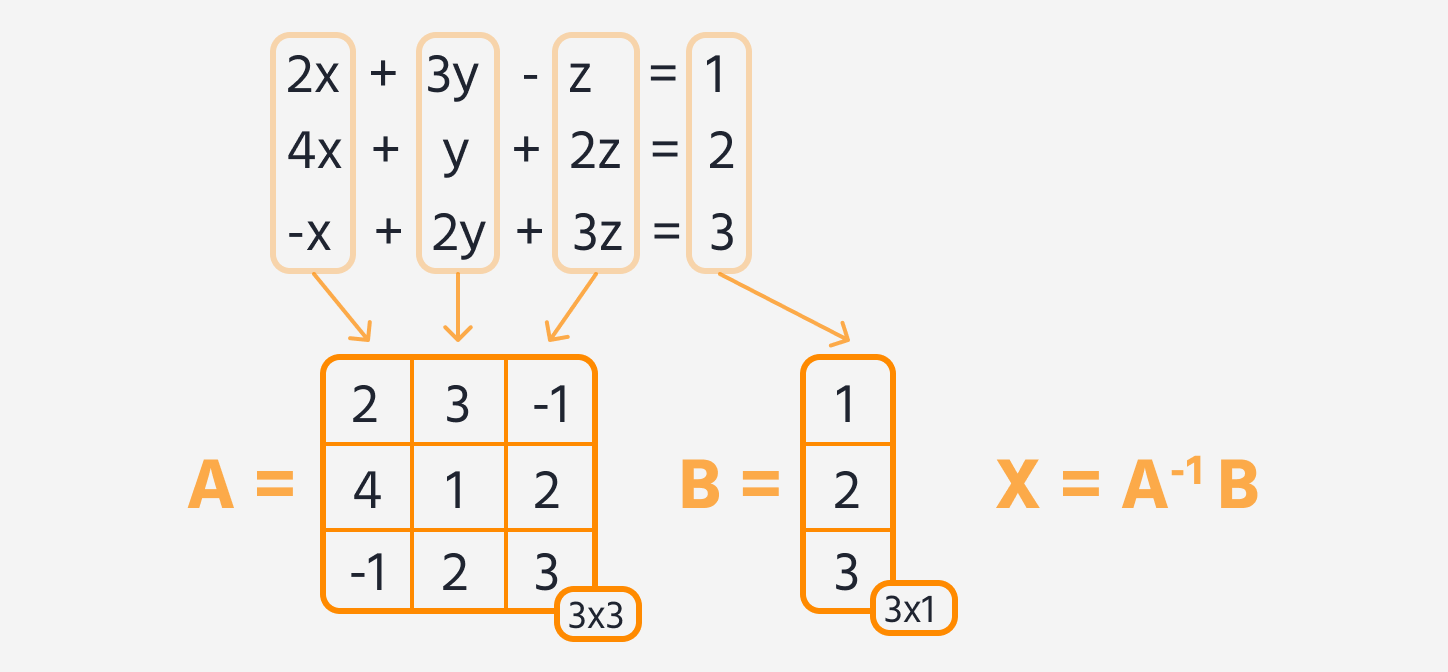
Representar el sistema de ecuaciones en forma matricial (separándolo en las matrices A y B).
Utilizar TensorFlow para encontrar la inversa de la matriz A.
Multiplicar la inversa de la matriz A por la matriz B para encontrar la matriz solución X, que contiene los valores de x, y y z.

Nota

El corte (slicing) en TensorFlow funciona de manera similar a NumPy. Por lo tanto, X[:, 0] recuperará todos los elementos de la columna en el índice 0. Abordaremos el tema del slicing más adelante en el curso.

Solución

¿Todo estuvo claro?

¡Gracias por tus comentarios!

Sección 1. Capítulo 9

single

Pregunte a AI

Pregunte lo que quiera o pruebe una de las preguntas sugeridas para comenzar nuestra charla

Awesome!

Completion rate improved to 5.56

Desliza para mostrar el menú

Operaciones de Álgebra Lineal

TensorFlow ofrece un conjunto de funciones dedicadas a las operaciones de álgebra lineal, facilitando las operaciones con matrices.

Multiplicación de Matrices

A continuación, un recordatorio rápido de cómo funciona la multiplicación de matrices.

Existen dos enfoques equivalentes para la multiplicación de matrices:

La función tf.matmul();
Usar el operador @.


              1234567891011121314
            
import tensorflow as tf

# Create two matrices
matrix1 = tf.constant([[1, 2], [3, 4], [2, 1]])
matrix2 = tf.constant([[2, 0, 2, 5], [2, 2, 1, 3]])

# Multiply the matrices
product1 = tf.matmul(matrix1, matrix2)
product2 = matrix1 @ matrix2

# Display tensors
print(product1)
print('-' * 50)
print(product2)

Nota

Multiplicar matrices de tamaño 3x2 y 2x4 dará como resultado una matriz de 3x4.

Inversión de matrices

Se puede obtener la inversa de una matriz utilizando la función tf.linalg.inv(). Además, verifiquemos una propiedad fundamental de la matriz inversa.


              123456789101112131415
            
import tensorflow as tf

# Create 2x2 matrix
matrix = tf.constant([[1., 2.], [3., 4.]])

# Compute the inverse of a matrix
inverse_mat = tf.linalg.inv(matrix)

# Check the result
identity = matrix @ inverse_mat

# Display tensors
print(inverse_mat)
print('-' * 50)
print(identity)

Nota

Transposición

Se puede obtener una matriz transpuesta utilizando la función tf.transpose().


              123456789101112
            
import tensorflow as tf

# Create a matrix 3x2
matrix = tf.constant([[1, 2], [3, 4], [2, 1]])

# Get the transpose of a matrix
transposed = tf.transpose(matrix)

# Display tensors
print(matrix)
print('-' * 40)
print(transposed)

Producto punto


              1234567891011121314
            
import tensorflow as tf

# Create two vectors
matrix1 = tf.constant([1, 2, 3, 4])
matrix2 = tf.constant([2, 0, 2, 5])

# Compute the dot product of two tensors
dot_product_axes1 = tf.tensordot(matrix1, matrix2, axes=1)
dot_product_axes0 = tf.tensordot(matrix1, matrix2, axes=0)

# Display tensors
print(dot_product_axes1)
print('-' * 40)
print(dot_product_axes0)

Nota

Tarea

Swipe to start coding

Contexto

Un sistema de ecuaciones lineales puede representarse en forma matricial utilizando la ecuación:

AX = B

Donde:

A es una matriz de coeficientes;
X es una matriz columna de variables;
B es una matriz columna que representa los valores en el lado derecho de las ecuaciones.

La solución de este sistema se puede encontrar usando la fórmula:

X = A^-1 B

Donde A^-1 es la inversa de la matriz A.

Objetivo

Dado un sistema de ecuaciones lineales, utilizar TensorFlow para resolverlo. Se proporciona el siguiente sistema de ecuaciones lineales:

2x + 3y - z = 1.
4x + y + 2z = 2.
-x + 2y + 3z = 3.

Representar el sistema de ecuaciones en forma matricial (separándolo en las matrices A y B).
Utilizar TensorFlow para encontrar la inversa de la matriz A.
Multiplicar la inversa de la matriz A por la matriz B para encontrar la matriz solución X, que contiene los valores de x, y y z.

Nota

El corte (slicing) en TensorFlow funciona de manera similar a NumPy. Por lo tanto, X[:, 0] recuperará todos los elementos de la columna en el índice 0. Abordaremos el tema del slicing más adelante en el curso.

Solución

Cambia al escritorio para practicar en el mundo realContinúe desde donde se encuentra utilizando una de las siguientes opciones

¿Todo estuvo claro?

¡Gracias por tus comentarios!

Sección 1. Capítulo 9

single

Operaciones Básicas: Álgebra Lineal

Operaciones de Álgebra Lineal

Multiplicación de Matrices

Inversión de matrices

Transposición

Producto punto

Contexto

Objetivo

Solución

Awesome!

Operaciones Básicas: Álgebra Lineal

Operaciones de Álgebra Lineal

Multiplicación de Matrices

Inversión de matrices

Transposición

Producto punto

Contexto

Objetivo

Solución