 Lineare Algebra
Lineare Algebra
Lineare Algebraoperationen
TensorFlow bietet eine Reihe von Funktionen für lineare Algebra-Operationen, die Matrixoperationen unkompliziert machen.
Matrixmultiplikation
Hier eine kurze Erinnerung daran, wie Matrixmultiplikation funktioniert.
Es gibt zwei gleichwertige Ansätze für die Matrixmultiplikation:
- Die Funktion
tf.matmul(); - Die Verwendung des Operators
@.
1234567891011121314import tensorflow as tf # Create two matrices matrix1 = tf.constant([[1, 2], [3, 4], [2, 1]]) matrix2 = tf.constant([[2, 0, 2, 5], [2, 2, 1, 3]]) # Multiply the matrices product1 = tf.matmul(matrix1, matrix2) product2 = matrix1 @ matrix2 # Display tensors print(product1) print('-' * 50) print(product2)
Die Multiplikation von Matrizen der Größe 3x2 und 2x4 ergibt eine Matrix der Größe 3x4.
Matrixinversion
Die Inverse einer Matrix kann mit der Funktion tf.linalg.inv() berechnet werden. Zusätzlich wird eine grundlegende Eigenschaft der inversen Matrix überprüft.
123456789101112131415import tensorflow as tf # Create 2x2 matrix matrix = tf.constant([[1., 2.], [3., 4.]]) # Compute the inverse of a matrix inverse_mat = tf.linalg.inv(matrix) # Check the result identity = matrix @ inverse_mat # Display tensors print(inverse_mat) print('-' * 50) print(identity)
Die Multiplikation einer Matrix mit ihrer Inversen ergibt eine Einheitsmatrix, die Einsen auf der Hauptdiagonalen und Nullen an allen anderen Stellen enthält. Darüber hinaus bietet das Modul tf.linalg eine breite Palette an linearen Algebra-Funktionen. Für weitere Informationen oder fortgeschrittene Operationen empfiehlt sich ein Blick in die offizielle Dokumentation.
Transponieren
Eine transponierte Matrix kann mit der Funktion tf.transpose() erzeugt werden.
123456789101112import tensorflow as tf # Create a matrix 3x2 matrix = tf.constant([[1, 2], [3, 4], [2, 1]]) # Get the transpose of a matrix transposed = tf.transpose(matrix) # Display tensors print(matrix) print('-' * 40) print(transposed)
Skalarprodukt
Das Skalarprodukt kann mit der Funktion tf.tensordot() berechnet werden. Durch Festlegen des Arguments axes kann ausgewählt werden, entlang welcher Achsen das Skalarprodukt berechnet wird. Zum Beispiel erhält man für zwei Vektoren mit axes=1 das klassische Skalarprodukt zwischen Vektoren. Wird hingegen axes=0 gesetzt, erhält man eine über die 0-Achse gebroadcastete Matrix:
1234567891011121314import tensorflow as tf # Create two vectors matrix1 = tf.constant([1, 2, 3, 4]) matrix2 = tf.constant([2, 0, 2, 5]) # Compute the dot product of two tensors dot_product_axes1 = tf.tensordot(matrix1, matrix2, axes=1) dot_product_axes0 = tf.tensordot(matrix1, matrix2, axes=0) # Display tensors print(dot_product_axes1) print('-' * 40) print(dot_product_axes0)
Wenn Sie zwei Matrizen mit passenden Dimensionen (NxM @ MxK, wobei NxM die Dimensionen der ersten Matrix und MxK die der zweiten darstellt) nehmen und das Skalarprodukt entlang axes=1 berechnen, wird im Wesentlichen eine Matrixmultiplikation durchgeführt.
Swipe to start coding
Hintergrund
Ein lineares Gleichungssystem kann in Matrixform durch die Gleichung dargestellt werden:
AX = B
Dabei gilt:
Aist eine Koeffizientenmatrix;Xist eine Spaltenmatrix der Variablen;Bist eine Spaltenmatrix, die die Werte auf der rechten Seite der Gleichungen darstellt.
Die Lösung dieses Systems kann mit folgender Formel gefunden werden:
X = A^-1 B
wobei A^-1 die Inverse der Matrix A ist.
Zielsetzung
Gegeben ist ein lineares Gleichungssystem, das mit TensorFlow gelöst werden soll. Das folgende Gleichungssystem ist gegeben:
2x + 3y - z = 1.4x + y + 2z = 2.-x + 2y + 3z = 3.
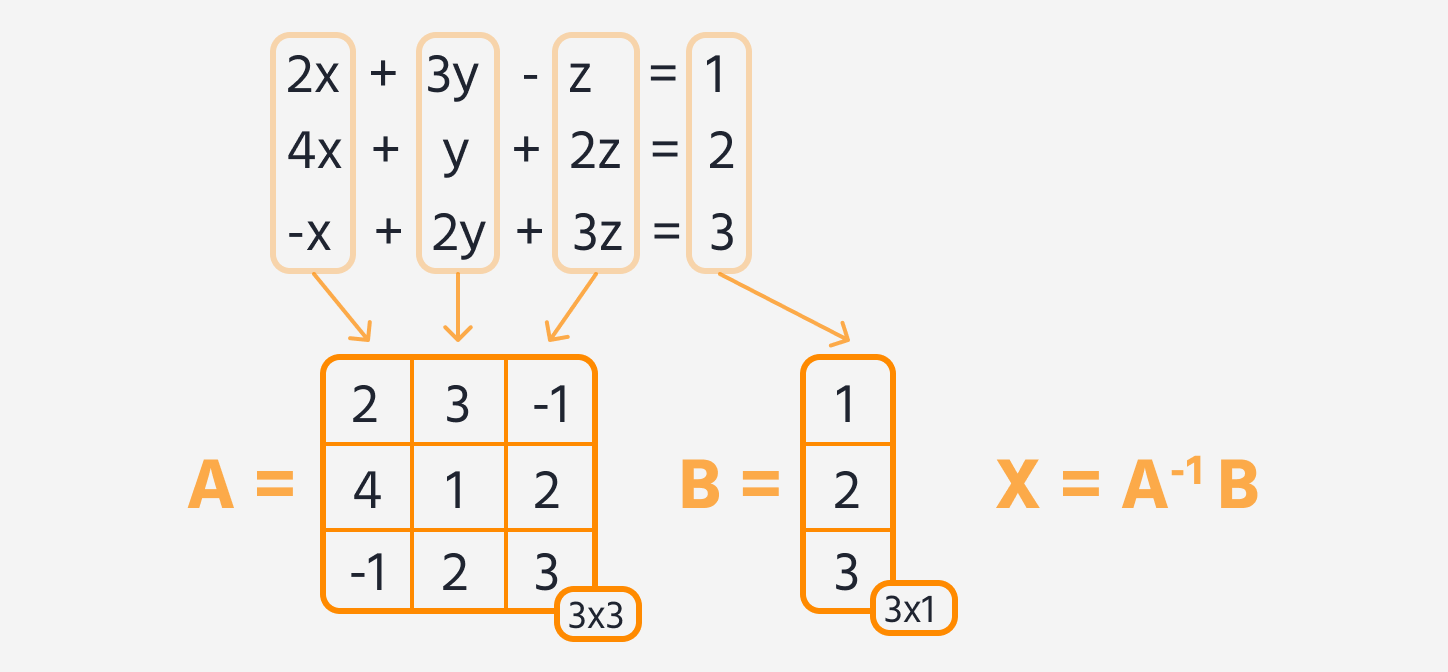
- Darstellung des Gleichungssystems in Matrixform (Aufteilung in die Matrizen
AundB). - Mit TensorFlow die Inverse der Matrix
Aberechnen. - Die Inverse der Matrix
Amit der MatrixBmultiplizieren, um die LösungsmatrixXzu erhalten, die die Werte fürx,yundzenthält.
Hinweis
Das Slicing in TensorFlow funktioniert ähnlich wie in NumPy. Daher ruft
X[:, 0]alle Elemente aus der Spalte mit dem Index0ab. Auf das Slicing gehen wir später im Kurs noch genauer ein.
Lösung
Danke für Ihr Feedback!
single
Fragen Sie AI
Fragen Sie AI

Fragen Sie alles oder probieren Sie eine der vorgeschlagenen Fragen, um unser Gespräch zu beginnen
Can you explain the difference between tf.matmul() and the @ operator?
How do I know when to use tf.tensordot() instead of tf.matmul()?
Can you provide more examples of matrix operations in TensorFlow?

Großartig!
Completion Rate verbessert auf 6.25 Lineare Algebra
Lineare Algebra
Swipe um das Menü anzuzeigen
Lineare Algebraoperationen
TensorFlow bietet eine Reihe von Funktionen für lineare Algebra-Operationen, die Matrixoperationen unkompliziert machen.
Matrixmultiplikation
Hier eine kurze Erinnerung daran, wie Matrixmultiplikation funktioniert.
Es gibt zwei gleichwertige Ansätze für die Matrixmultiplikation:
- Die Funktion
tf.matmul(); - Die Verwendung des Operators
@.
1234567891011121314import tensorflow as tf # Create two matrices matrix1 = tf.constant([[1, 2], [3, 4], [2, 1]]) matrix2 = tf.constant([[2, 0, 2, 5], [2, 2, 1, 3]]) # Multiply the matrices product1 = tf.matmul(matrix1, matrix2) product2 = matrix1 @ matrix2 # Display tensors print(product1) print('-' * 50) print(product2)
Die Multiplikation von Matrizen der Größe 3x2 und 2x4 ergibt eine Matrix der Größe 3x4.
Matrixinversion
Die Inverse einer Matrix kann mit der Funktion tf.linalg.inv() berechnet werden. Zusätzlich wird eine grundlegende Eigenschaft der inversen Matrix überprüft.
123456789101112131415import tensorflow as tf # Create 2x2 matrix matrix = tf.constant([[1., 2.], [3., 4.]]) # Compute the inverse of a matrix inverse_mat = tf.linalg.inv(matrix) # Check the result identity = matrix @ inverse_mat # Display tensors print(inverse_mat) print('-' * 50) print(identity)
Die Multiplikation einer Matrix mit ihrer Inversen ergibt eine Einheitsmatrix, die Einsen auf der Hauptdiagonalen und Nullen an allen anderen Stellen enthält. Darüber hinaus bietet das Modul tf.linalg eine breite Palette an linearen Algebra-Funktionen. Für weitere Informationen oder fortgeschrittene Operationen empfiehlt sich ein Blick in die offizielle Dokumentation.
Transponieren
Eine transponierte Matrix kann mit der Funktion tf.transpose() erzeugt werden.
123456789101112import tensorflow as tf # Create a matrix 3x2 matrix = tf.constant([[1, 2], [3, 4], [2, 1]]) # Get the transpose of a matrix transposed = tf.transpose(matrix) # Display tensors print(matrix) print('-' * 40) print(transposed)
Skalarprodukt
Das Skalarprodukt kann mit der Funktion tf.tensordot() berechnet werden. Durch Festlegen des Arguments axes kann ausgewählt werden, entlang welcher Achsen das Skalarprodukt berechnet wird. Zum Beispiel erhält man für zwei Vektoren mit axes=1 das klassische Skalarprodukt zwischen Vektoren. Wird hingegen axes=0 gesetzt, erhält man eine über die 0-Achse gebroadcastete Matrix:
1234567891011121314import tensorflow as tf # Create two vectors matrix1 = tf.constant([1, 2, 3, 4]) matrix2 = tf.constant([2, 0, 2, 5]) # Compute the dot product of two tensors dot_product_axes1 = tf.tensordot(matrix1, matrix2, axes=1) dot_product_axes0 = tf.tensordot(matrix1, matrix2, axes=0) # Display tensors print(dot_product_axes1) print('-' * 40) print(dot_product_axes0)
Wenn Sie zwei Matrizen mit passenden Dimensionen (NxM @ MxK, wobei NxM die Dimensionen der ersten Matrix und MxK die der zweiten darstellt) nehmen und das Skalarprodukt entlang axes=1 berechnen, wird im Wesentlichen eine Matrixmultiplikation durchgeführt.
Swipe to start coding
Hintergrund
Ein lineares Gleichungssystem kann in Matrixform durch die Gleichung dargestellt werden:
AX = B
Dabei gilt:
Aist eine Koeffizientenmatrix;Xist eine Spaltenmatrix der Variablen;Bist eine Spaltenmatrix, die die Werte auf der rechten Seite der Gleichungen darstellt.
Die Lösung dieses Systems kann mit folgender Formel gefunden werden:
X = A^-1 B
wobei A^-1 die Inverse der Matrix A ist.
Zielsetzung
Gegeben ist ein lineares Gleichungssystem, das mit TensorFlow gelöst werden soll. Das folgende Gleichungssystem ist gegeben:
2x + 3y - z = 1.4x + y + 2z = 2.-x + 2y + 3z = 3.

- Darstellung des Gleichungssystems in Matrixform (Aufteilung in die Matrizen
AundB). - Mit TensorFlow die Inverse der Matrix
Aberechnen. - Die Inverse der Matrix
Amit der MatrixBmultiplizieren, um die LösungsmatrixXzu erhalten, die die Werte fürx,yundzenthält.
Hinweis
Das Slicing in TensorFlow funktioniert ähnlich wie in NumPy. Daher ruft
X[:, 0]alle Elemente aus der Spalte mit dem Index0ab. Auf das Slicing gehen wir später im Kurs noch genauer ein.
Lösung
Danke für Ihr Feedback!
single