 Gradient Tape
Gradient Tape
Gradient Tape
Understanding fundamental tensor operations allows progression to streamlining and accelerating these processes using built-in TensorFlow features. The first of these advanced tools to explore is Gradient Tape.
What is Gradient Tape?
This chapter delves into one of the fundamental concepts in TensorFlow, the Gradient Tape. This feature is essential for understanding and implementing gradient-based optimization techniques, particularly in deep learning.
Gradient Tape in TensorFlow is a tool that records operations for automatic differentiation. When operations are performed inside a Gradient Tape block, TensorFlow keeps track of all the computations that happen. This is particularly useful for training machine learning models, where gradients are needed to optimize model parameters.
Essentially, a gradient is a set of partial derivatives.
Usage of Gradient Tape
To use Gradient Tape, follow these steps:
- Create a Gradient Tape block: use
with tf.GradientTape() as tape:. Inside this block, all the computations are tracked; - Define the computations: perform operations with tensors within the block (e.g. define a forward pass of a neural network);
- Compute gradients: use
tape.gradient(target, sources)to calculate the gradients of the target with respect to the sources.
Simple Gradient Calculation
A simple example to understand this better.
123456789101112131415import tensorflow as tf # Define input variables x = tf.Variable(3.0) # Start recording the operations with tf.GradientTape() as tape: # Define the calculations y = x * x # Extract the gradient for the specific input (`x`) grad = tape.gradient(y, x) print(f'Result of y: {y}') print(f'The gradient of y with respect to x is: {grad.numpy()}')
This code calculates the gradient of y = x^2 at x = 3. This is the same as the partial derivative of y with respect to x.
Several Partial Derivatives
When output is influenced by multiple inputs, a partial derivative can be computed with respect to each of these inputs (or just a selected few). This is achieved by providing a list of variables as the sources parameter.
The output from this operation will be a corresponding list of tensors, where each tensor represents the partial derivative with respect to each of the variables specified in sources.
1234567891011121314151617import tensorflow as tf # Define input variables x = tf.Variable(tf.fill((2, 3), 3.0)) z = tf.Variable(5.0) # Start recording the operations with tf.GradientTape() as tape: # Define the calculations y = tf.reduce_sum(x * x + 2 * z) # Extract the gradient for the specific inputs (`x` and `z`) grad = tape.gradient(y, [x, z]) print(f'Result of y: {y}') print(f"The gradient of y with respect to x is:\n{grad[0].numpy()}") print(f"The gradient of y with respect to z is: {grad[1].numpy()}")
This code computes the gradient of the function y = sum(x^2 + 2*z) for given values of x and z. In this example, the gradient of x is shown as a 2D tensor, where each element corresponds to the partial derivative of the respective value in the original x matrix.
For additional insights into Gradient Tape capabilities, including higher-order derivatives and extracting the Jacobian matrix, refer to the official TensorFlow documentation.
Swipe to start coding
Your goal is to compute the gradient (derivative) of a given mathematical function at a specified point using TensorFlow's Gradient Tape. The function and point will be provided, and you will see how to use TensorFlow to find the gradient at that point.
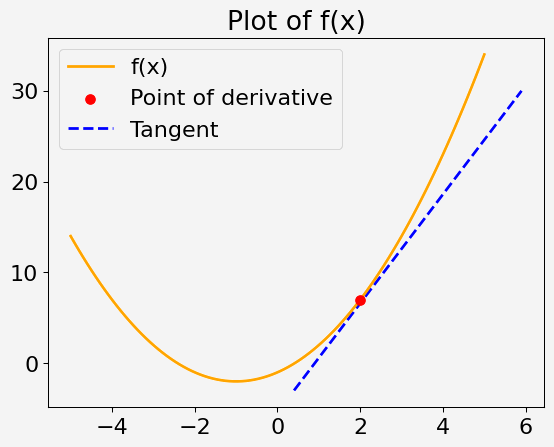
Consider a quadratic function of a single variable x, defined as:
f(x) = x^2 + 2x - 1
Your task is to calculate the derivative of this function at x = 2.
Steps
- Define the variable
xat the point where you want to compute the derivative. - Use Gradient Tape to record the computation of the function
f(x). - Calculate the gradient of
f(x)at the specified point.
Note
Gradient can only be computed for values of floating-point type.
Solution
Thanks for your feedback!
single
Ask AI
Ask AI

Ask anything or try one of the suggested questions to begin our chat

Awesome!
Completion rate improved to 6.25 Gradient Tape
Gradient Tape
Swipe to show menu
Gradient Tape
Understanding fundamental tensor operations allows progression to streamlining and accelerating these processes using built-in TensorFlow features. The first of these advanced tools to explore is Gradient Tape.
What is Gradient Tape?
This chapter delves into one of the fundamental concepts in TensorFlow, the Gradient Tape. This feature is essential for understanding and implementing gradient-based optimization techniques, particularly in deep learning.
Gradient Tape in TensorFlow is a tool that records operations for automatic differentiation. When operations are performed inside a Gradient Tape block, TensorFlow keeps track of all the computations that happen. This is particularly useful for training machine learning models, where gradients are needed to optimize model parameters.
Essentially, a gradient is a set of partial derivatives.
Usage of Gradient Tape
To use Gradient Tape, follow these steps:
- Create a Gradient Tape block: use
with tf.GradientTape() as tape:. Inside this block, all the computations are tracked; - Define the computations: perform operations with tensors within the block (e.g. define a forward pass of a neural network);
- Compute gradients: use
tape.gradient(target, sources)to calculate the gradients of the target with respect to the sources.
Simple Gradient Calculation
A simple example to understand this better.
123456789101112131415import tensorflow as tf # Define input variables x = tf.Variable(3.0) # Start recording the operations with tf.GradientTape() as tape: # Define the calculations y = x * x # Extract the gradient for the specific input (`x`) grad = tape.gradient(y, x) print(f'Result of y: {y}') print(f'The gradient of y with respect to x is: {grad.numpy()}')
This code calculates the gradient of y = x^2 at x = 3. This is the same as the partial derivative of y with respect to x.
Several Partial Derivatives
When output is influenced by multiple inputs, a partial derivative can be computed with respect to each of these inputs (or just a selected few). This is achieved by providing a list of variables as the sources parameter.
The output from this operation will be a corresponding list of tensors, where each tensor represents the partial derivative with respect to each of the variables specified in sources.
1234567891011121314151617import tensorflow as tf # Define input variables x = tf.Variable(tf.fill((2, 3), 3.0)) z = tf.Variable(5.0) # Start recording the operations with tf.GradientTape() as tape: # Define the calculations y = tf.reduce_sum(x * x + 2 * z) # Extract the gradient for the specific inputs (`x` and `z`) grad = tape.gradient(y, [x, z]) print(f'Result of y: {y}') print(f"The gradient of y with respect to x is:\n{grad[0].numpy()}") print(f"The gradient of y with respect to z is: {grad[1].numpy()}")
This code computes the gradient of the function y = sum(x^2 + 2*z) for given values of x and z. In this example, the gradient of x is shown as a 2D tensor, where each element corresponds to the partial derivative of the respective value in the original x matrix.
For additional insights into Gradient Tape capabilities, including higher-order derivatives and extracting the Jacobian matrix, refer to the official TensorFlow documentation.
Swipe to start coding
Your goal is to compute the gradient (derivative) of a given mathematical function at a specified point using TensorFlow's Gradient Tape. The function and point will be provided, and you will see how to use TensorFlow to find the gradient at that point.
Consider a quadratic function of a single variable x, defined as:
f(x) = x^2 + 2x - 1
Your task is to calculate the derivative of this function at x = 2.
Steps
- Define the variable
xat the point where you want to compute the derivative. - Use Gradient Tape to record the computation of the function
f(x). - Calculate the gradient of
f(x)at the specified point.
Note
Gradient can only be computed for values of floating-point type.

Solution
Thanks for your feedback!
single